1. Introduction▲
CRC veut dire Cyclic Redundancy Code
Le calcul de CRC permet au récepteur d'un message de verifier que les données transmises ne contiennent pas d'erreurs. Pour faire
cela, l'émetteur du message calcule une valeur "CheckSum" qui est fonction du contenu du message, puis l'ajoute à la fin du message.
Le récepteur fait le même calcul, et contôle que le "CheckSum" a la même valeur que celui de l'émetteur.
Un programme écrit en C++Builder vous permettra d'effectuer des tests de calcul. Nous écrirons une version dite " low speed "
de calcul des CRC en langage C.
2. Calcul d'une somme simple▲
On décide de faire la somme des valeurs numériques de tous les caractères du message, d'appliquer un module 256 au résultat pour obtenir une valeur sur 8 Bits, puis de l'ajouter à la fin du message. Le récepteur utilise la même technique et compare le résultat à celui qui est attaché au message, afin de voir si il a été correctement reçu ou pas.
typedef unsigned int TU_int32; // Mot de 32 bit non signé
typedef unsigned short int TU_int16; // Mot de 16 bits non signé
typedef unsigned char TU_int8; // Mot de 8 Bits non signéTU_int8 __fastcall CalcSomme(AnsiString Message)
{
TU_int8 iuResult = 0; // Resultat sur 8 bits
//--- Calcul de la somme, le premier caractère est en position 1
for (int i = 1; i <= Message.Length(); i++)
iuResult += Message[i];
//--- Modulo Valeur Maxi sur 8 Bits
return (iuResult %= 0xFF);
}
Démarrer le programme CalcCRC.
Sélectionner dans le combo type de calcul " Somme simple modulo 256 ", entrer une chaîne de caractères et cliquer sur calculer.
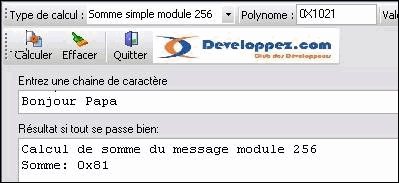
Entrer la chaîne "Bonjour Papa". La somme est 0x81.
Entrer la chaîne "Bonjour Papi". La somme est 0x89.
Le message est corrompu, cependant le récepteur peut le détecter en comparant la somme transmise (0x81) à la somme qu'il a calculé
(0x89) et demander une nouvelle transmission. Bien évidemment, si la somme elle-même est corrompue, un message correctement transmis
peut être identifié comme corrompu. Cependant, ce n'est pas très grave, car le message est reconnu comme corrompu. Ce qui peut être
dangereux, c'est que le message soit corrompu et que le résultat du calcul de contrôle soit correct. Malheureusement, cette possibilité
est inévitable et on ne peut qu'essayer d'en réduire la probabilité en améliorant le calcul de la somme.
3. Le besoin de complexité ▲
Dans le paragraphe précédent, nous avons vu comment le message corrompu a été détecté par le simple calcul de la somme des
caractères et un modulo 256. Le problème avec cet algorithme est qu'il est trop simple, et que la somme peut être juste alors qu'il
y a bien une corruption du message.
Reprenons notre exemple :
Entrer la chaine "Bonjour Papa". La somme est 0x81.
Entrer la chaine "Banjour Papo". la somme est 0x81.
Le message n'est pas le même, mais le calcul de la somme donne la même valeur. Dans cet exemple, le deuxième message contient exactement
les mêmes caractères, mais dans un ordre différent, ce qui produit la même somme. Pour améliorer le calcul de la somme, on peut par
exemple effectuer le calcul sur 2 bytes au lieu de 1 byte. En utilisant 65536 comme modulo, ce qui permettrait de ramener la
probabilité de l'échec de 1/256 à 1/65536. Malgré l'ajout d'un byte au contrôle, cette somme produira toujours des erreurs, car la
formule utilisée n'est pas suffisamment aléatoire. Avec une adition simple des caractères du message, chaque byte entrant affecte
approximativement un seul byte de l'addition. Ce problème peut être résolu par l'utilisation d'une formule de calcul plus sophistiquée
où chaque byte en entrée peut avoir un effet sur l'ensemble du résultat de la somme.
On constate donc qu'il y a au moins deux aspects à prendre en compte pour réaliser une fonction de somme correcte.
1 - La largeur du code de contrôle pour réduire la probabilité d'erreur. Par exemple sur 32 bits la probabilité et de (½^32)
2 - Une formule qui donne à chaque byte d'entrée le potentiel de changer la valeur du code de contrôle.
Le terme "Somme ou Checksum" a été employé pour décrire la formule de contrôle, mais a maintenant pris une signification plus
générale entourant des algorithmes plus sophistiqués tels que le CRC. Les algorithmes de CRC que l'on va décrire satisfont très bien
la deuxième condition, et peuvent être configurés pour fonctionner avec plusieurs largeurs de somme. Ils sont basés sur de simples
calculs d'arithmétique modulaire.
4. La division binaire▲
L'idée fondamentale des algorithmes de CRC est simplement de traiter le message comme une grande valeur numérique, de le diviser par
une valeur fixe, de prendre le reste de la division en tant que somme de contrôle.
La valeur numérique du message est bien supérieure à la valeur maximum d'un mot de 32 bits de large. Nous allons donc faire la division
Byte par Byte mais cette fois en binaire. La division binaire ressemble beaucoup à une division euclidienne comme on
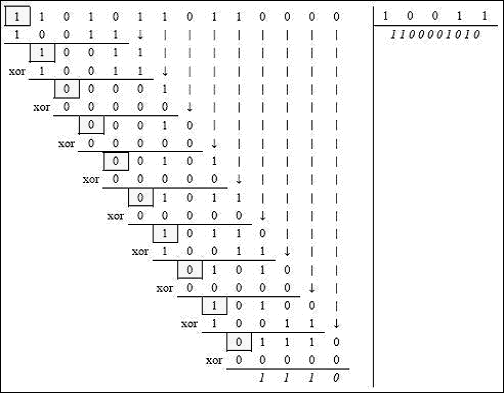
l'apprend à l'école, le résultat donne un quotient et un reste. Le calcul bit à bit se fait par un "ou exclusif" (encore appelé XOR).
| XOR | 1 | 0 |
|---|---|---|
| 1 | 0 | 1 |
| 0 | 1 | 0 |
La division binaire
On sélectionne le bit de poids fort du dividende, ici (1), il sera le bit de poids fort du quotient. Maintenant, on peut faire
(1 x diviseur) = 10011. On fait ensuite un XOR entre le dividende et ce résultat qui est décalé de suffisamment de bits pour commencer
au début du dividende. Ensuite, on ajoute au résultat de l'opération le bit suivant correspondant au dividende.
L'opération s'enchaîne ainsi de suite. On sélectionne le bit de poids fort du résultat précédemment trouvé, ici, c'est un 1. On lui
applique un XOR avec 10011. Le résultat sera 0000, auquel on fera descendre 1, ce qui donne 00001. Le bit de poids fort est un 0, donc
(0x diviseur)=00000. On refait l'opération avec le XOR. Ces opérations seront réalisées jusqu'à ce qu'on ne puisse plus " descendre "
de bit depuis le dividende, donc on réalise (Taille du dividende-Taille du diviseur+1) opérations (en fait, la taille correspondant au
nombre de bits).
5. Les polynômes ▲
Le mot qui revient souvent en traitant les algorithmes de CRC est " POLYNOME ". On dira qu'un algorithme de CRC donné utilise un
polynôme particulier. Comme dans la division binaire, le résultat donne un quotient et un reste, mais vus comme un polynôme avec un
coefficient binaires.
Un polynôme P(x) est une fonction de x de la forme :
| P(x) = FN * XN + FN-1 * XN-1 + ... + F0 * X0 |
Les parties Fi sont membres de l'ensemble des réels et sont appelées " Facteur " d'indice i. N est le " Degré " du polynôme
(l'exposant le plus élevé). La partie Fk * Xk est appelée terme de degré k du polynôme.
La division de polynômes est une opération mathématique donnant comme résultat le calcul de deux valeurs polynomiales : un Quotient
et un Reste (division euclidienne). Le degré du Reste est égal au plus à celui du Diviseur moins 1.
| Dividende = Quotient * Diviseur + Reste |
Exemple:
| 23 (Décimale) = 17 (Hexa) = 10111 (Binaire) |
Ce qui correspond au polynôme :
| 1*x^4 + 0*x^3 + 1*x^2 + 1*x^1 + 1*x^0 |
| Ou plus simplement |
| x^4 + x^2 + x^1 + x^0 |
En utilisant cette technique, le message, et le diviseur peuvent être représentés comme des polynômes et nous pouvons faire notre calcul juste comme avant. Par exemple, pour multiplier 1101 par 1011. Nous pouvons le faire simplement en multipliant les polynômes
| (x^3 + x^2 + x^0) (x^3 + x^1 + x^0) |
| = |
| (x^6 + x^4 + x^3+ x^5 + x^3 + x^2+ x^3 + x^1 + x^0) |
| = |
| x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0 |
6. Fonctionnement▲
Mettre en application un algorithme de calcul de CRC revient à effectuer une division. Mais nous ne pouvons pas directement effectuer cette division. Nous allons donc effectuer une division, octet par octet, de la trame d'entrée. Le récepteur de la trame divisera la somme des octets de la trame + la valeur du CRC par le même polynôme. Si le reste est NULL, c'est que la trame est correctement reçue.
Le choix du polynôme générateur est fonction de la qualité recherchée : le plus simple est d'utiliser ceux qui sont déjà définis.
| CRC16 CCITT | x16 + x12 + x5 + 1 |
| CRC32 (Ethernet) | x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x1 + 1 |
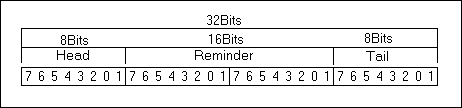
Donc pour effectuer cette division, nous allons créer un " Registre de division " auquel nous passerons les octets de la trame. Un octet = 8 Bits, Bit7 = MSB, Bit0 = LSB. Par exemple avec un registre de 4Bits de large.
| 3 | 2 | 1 | 0 | Bits | |
| Sortie | Entrée | ||||
| 1 | 0 | 0 | 1 | 1 | Polynôme |
Charger le Registre de division avec des 0
Faire
Décaler le registre de 1 bit vers la gauche
Si (Bit en sortie = 1) Alors
Registre = Registre XOR Polynôme
FinSi
Tant Que (Il reste des bits)A la fin du calcul, le registre de division contient le reste de la division.
7. Implémentation d'un registre de division en langage C▲
typedef union {
TU_int32 Value; // Valeur sur 32 Bit
struct {
TU_int8 Tail; // 8 bits Entrée du registre
TU_int16 Remainder; // 16 bits Reste de la division
TU_int8 Head; // 8 bits Sortie du registre
} Part;
}TCRC16_Part;
// Registre de Division
static TCRC16_Part _CCITTCrc16;const int CRC_POLYNOMIAL = 0x1021; // Specifique CRC16-CCITT
const int CRC_INIT_VALUE = 0xFFFF; // Specifique CRC16-CCITTvoid __fastcall OneByteCrc16(TU_int8 Byte)
{
int ByteCnt = 8;
//--- Stocker la nouvelle valeur a la fin
_CCITTCrc16.Part.Tail = Byte;
//--- Test des bit du Byte
do {
//--- Décalage de 1 bit vers la Gauche
_CCITTCrc16.Value <<= 1;
//--- Si le bit est à 1
if (_CCITTCrc16.Part.Head & 0x01)
//--- XOR avec le POLYNOME
_CCITTCrc16.Part.Remainder ^= CRC_POLYNOMIAL;
} while (--ByteCnt);
}TU_int16 __fastcall StringToCCITTCrc16(AnsiString S)
{
//--- Reste de la division initiale
_CCITTCrc16.Part.Remainder = CRC_INIT_VALUE;
//--- Boucle de lecture de la chaine
for (int i = 1; i <= S.Length(); i++)
OneByteCrc16(S[i]);
//--- Ajouter 0
OneByteCrc16(0x00);
//--- Polynome = 16
OneByteCrc16(0x00);
//--- Retourne le reste de la division sur 16 bits du CRC16
return _CCITTCrc16.Part.Remainder;
}
Avec un dessin on comprend mieux
| Registre de division |
_CCITTCrc16.Part.Remainder = CRC_INIT_VALUE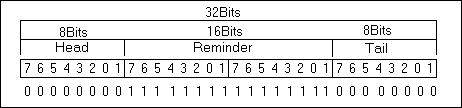
_CCITTCrc16.Part.Tail = Byte;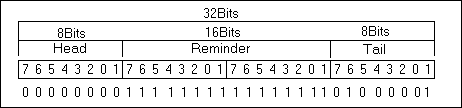
_CCITTCrc16.Value <<= 1;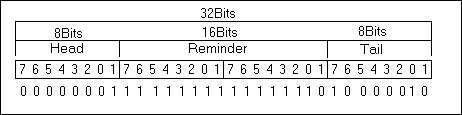
if (_CCITTCrc16.Part.Head & 0x01)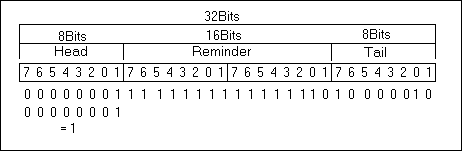
_CCITTCrc16.Part.Remainder ^= CRC_POLYNOMIAL;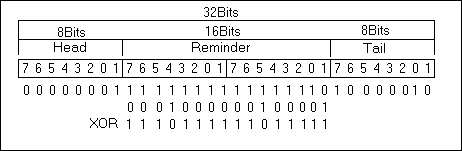
| Nouvelle valeur du registre |
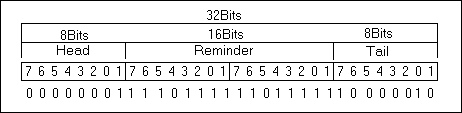
Et ainsi de suite pour les 8 bits de chaque octet de la trame.
8. Programme de test▲
Démarrer le programme CalcCRC.
Sélectionner dans le combo type de calcul CRC16 selon CCITT
entrer une chaîne de caractères est cliquer sur calculer
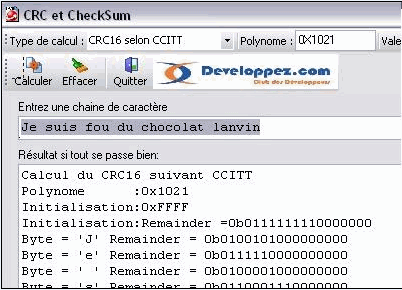
Le programme affiche la valeur calculée et le reste de la division pour chaque caractère en entrée.
Vous pouvez également effectuer des calculs suivant un polynôme spécifique. Dans le combo type de calcul, sélectionner
" CRC16 selon paramètre ", entrer une valeur pour le polynôme ainsi que pour la valeur initiale.
9. Téléchargement▲
10. Conclusion▲
A suivre la version de calcul des CRC dit "Table-Driven", dès que j'aurais un peu plus de temps.
Bonne lecture est à bientôt sur developpez.com
Merci à BWP-Necromance pour son aide.
Merci à Rupella pour la correction sur le dessin, aprés un XOR
DVSoft